単回帰分析 - 各種モデル(直線/曲線回帰)の比較!
Updated:
これまで Ruby で Array クラスを拡張して単回帰直線や各種単回帰曲線を計算してみました。
今回、それぞれの回帰モデル間にどのような違いがあるのか、グラフを並べて比較してみました。
0. 前提条件
- LMDE 3 (Linux Mint Debian Edition 3; 64bit) での作業を想定。
- Ruby 2.6.3 での作業を想定。
1. 各種単回帰モデルについて
過去記事を参照。
- Ruby - Array クラス拡張で単回帰直線計算(Ver.2)!
- Ruby - Array クラス拡張で単回帰曲線計算(Ver.2)!
- Ruby - Array クラス拡張で単回帰曲線(3次回帰モデル)計算!
- Ruby - Array クラス拡張で単回帰曲線(4次回帰モデル)計算!
- Ruby - Array クラス拡張で単回帰曲線(ルート回帰モデル)計算!
- Ruby - Array クラス拡張で単回帰曲線(自然対数回帰モデル)計算!
- Ruby - Array クラス拡張で単回帰曲線(分数(逆数)回帰モデル)計算!
- Ruby - Array クラス拡張で単回帰曲線(べき乗回帰モデル)計算!
- Ruby - Array クラス拡張で単回帰曲線(指数(ab指数)回帰モデル)計算!
- Ruby - Array クラス拡張で単回帰曲線(e指数回帰モデル)計算!
2. 使用する説明変数と目的変数
以下のような、体重(kg)と身長(cm)のようなデータ。
説明変数 X = {83, 71, 64, 69, 69, 64, 68, 59, 81, 91, 57, 65, 58, 62}
目的変数 Y = {183, 168, 171, 178, 176, 172, 165, 158, 183, 182, 163, 175,164, 175}
3. 各種グラフ
【直線回帰モデル】 \(y=a+bx\)
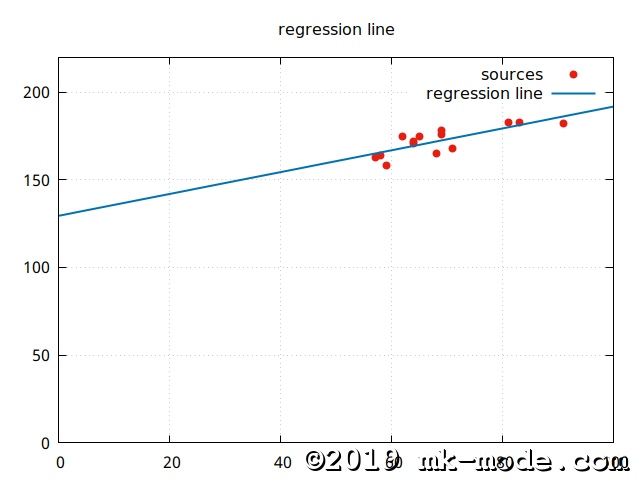
【2次曲線回帰モデル】 \(y=a+bx+cx^2\)
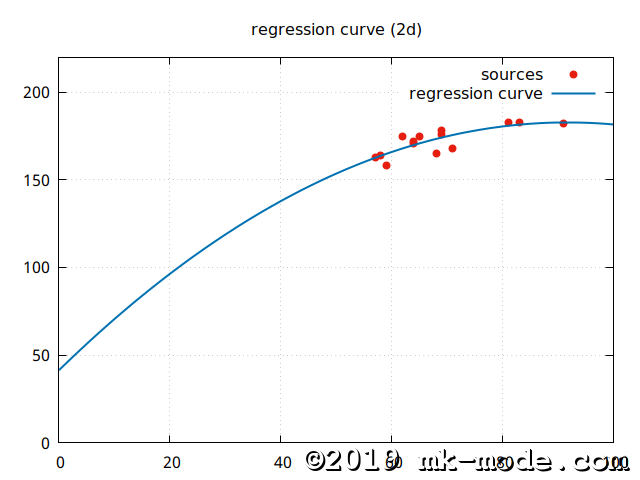
【3次曲線回帰モデル】 \(y=a+bx+cx^2+dx^3\)
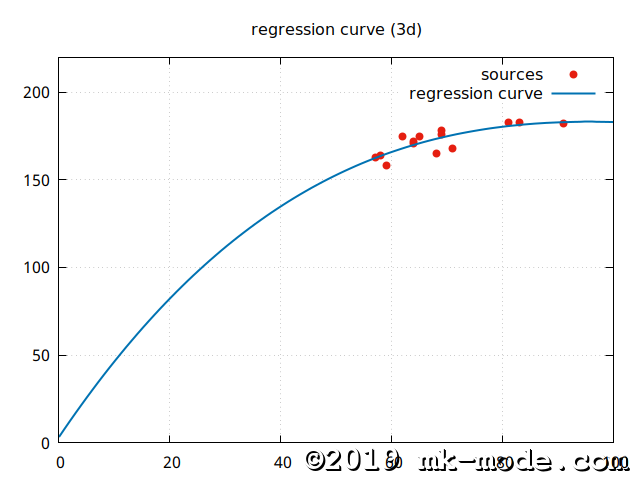
【4次曲線回帰モデル】 \(y=a+bx+cx^2+dx^3+ex^4\)
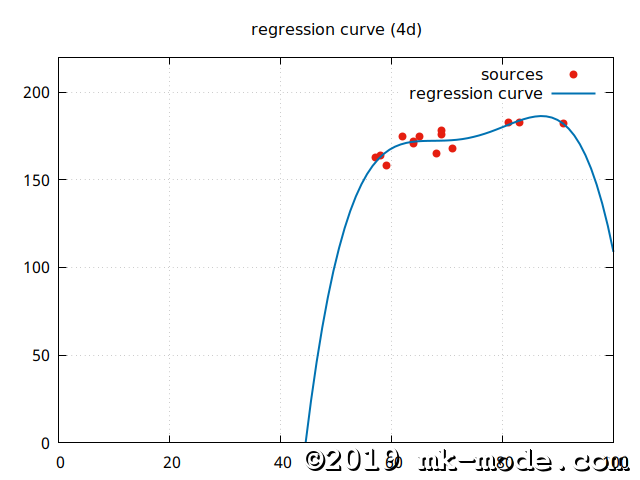
【ルート回帰モデル】 \(y=a+b\sqrt{x}\)
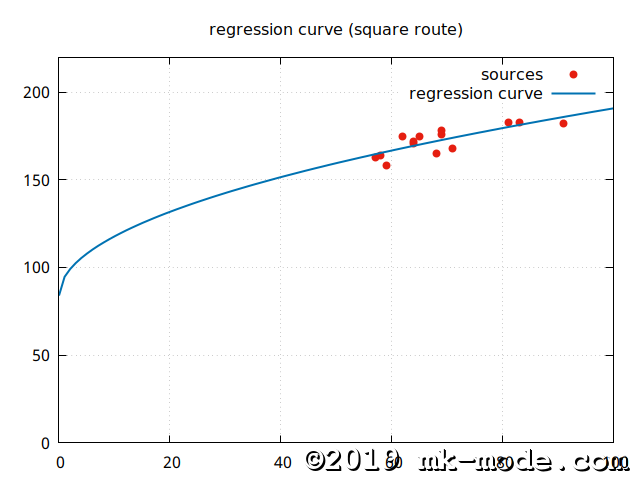
【自然対数回帰モデル】 \(y=a+b\log_e{x}\)
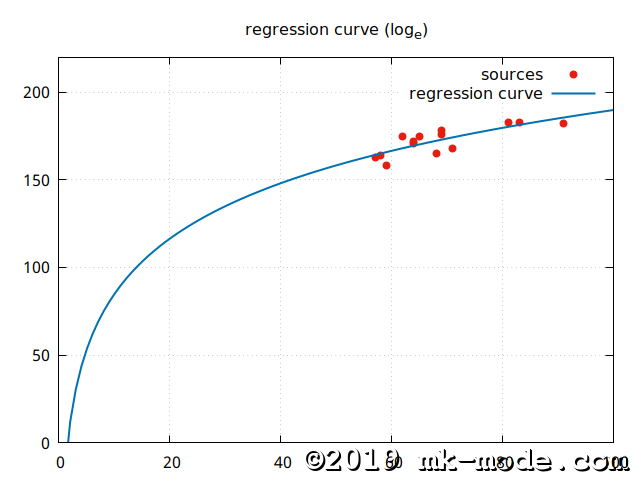
【分数(逆数)回帰モデル】 \(\displaystyle y=a+\frac{b}{x}\)
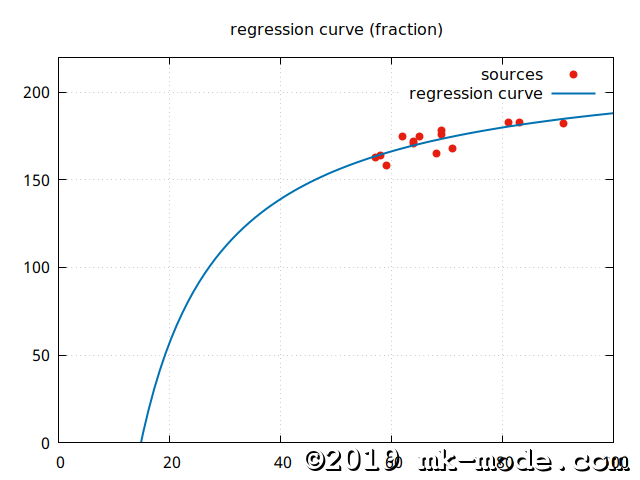
【べき乗回帰モデル】 \(y=ax^b\)
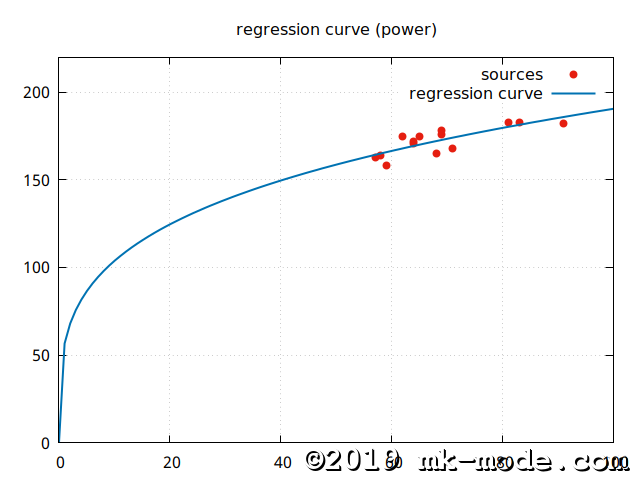
【指数(ab指数)回帰モデル】 \(y=ab^x\)
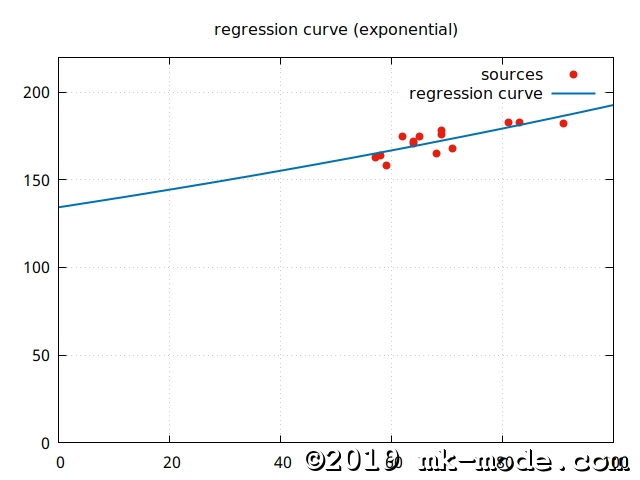
【e指数回帰モデル】 \(y=ae^{bx}\)
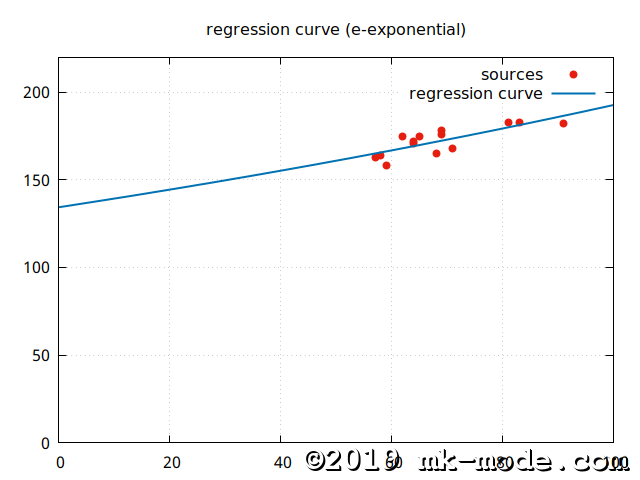
以上。

Comments