Fortran - 単回帰分析(2次曲線回帰)の決定係数計算!
Updated:
Fortran 95 で2つの単回帰分析(2次曲線回帰)の決定係数を計算してみました。
過去には Ruby で Array クラスを拡張して行なっています。
0. 前提条件
- LMDE 3 (Linux Mint Debian Edition 3; 64bit) での作業を想定。
- GCC 6.3.0 (GFortran 6.3.0) でのコンパイルを想定。
1. 決定係数について
当ブログ過去記事を参照のこと。
2. ソースコードの作成
- 以下のソースコードでは2種の方法で決定係数を計算している。
File: coefficient_of_determination_2d.f95
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
!****************************************************
! 単回帰分析(2次曲線回帰)の決定係数計算!
!
! date name version
! 2019.03.31 mk-mode.com 1.00 新規作成
!
! Copyright(C) 2019 mk-mode.com All Rights Reserved.
!****************************************************
!
module const
! SP: 単精度(4), DP: 倍精度(8)
integer, parameter :: SP = kind(1.0)
integer(SP), parameter :: DP = selected_real_kind(2 * precision(1.0_SP))
end module const
module comp
use const
implicit none
private
public :: calc_reg_curve
contains
! 単回帰曲線(2次回帰)計算
!
! :param(in) real(8) x(:): 説明変数配列
! :param(in) real(8) y(:): 目的変数配列
! :param(out) real(8) a: 係数 a
! :param(out) real(8) b: 係数 b
! :param(out) real(8) b: 係数 c
subroutine calc_reg_curve(x, y, a, b, c)
implicit none
real(DP), intent(in) :: x(:), y(:)
real(DP), intent(out) :: a, b, c
integer(SP) :: size_x, size_y, i
real(DP) :: m_x, m_x2, m_x3, m_x4, m_xy, m_x2y, m_y
real(DP) :: s_xx, s_xy, s_xx2, s_x2x2, s_x2y
size_x = size(x)
size_y = size(y)
if (size_x == 0 .or. size_y == 0) then
print *, "[ERROR] array size == 0"
stop
end if
if (size_x /= size_y) then
print *, "[ERROR] size(X) != size(Y)"
stop
end if
m_x = sum(x) / size_x ! avg(X)
m_y = sum(y) / size_y ! avg(Y)
m_x2 = sum(x * x) / size_x ! avg(X^2)
m_x3 = sum(x * x * x) / size_x ! avg(X^3)
m_x4 = sum(x * x * x * x) / size_x ! avg(X^4)
m_xy = sum(x * y) / size_x ! avg(X * Y)
m_x2y = sum(x * x * y) / size_x ! avg(X-2 * Y)
s_xx = m_x2 - m_x * m_x ! Sxx
s_xy = m_xy - m_x * m_y ! Sxy
s_xx2 = m_x3 - m_x * m_x2 ! Sxx2
s_x2x2 = m_x4 - m_x2 * m_x2 ! Sx2x2
s_x2y = m_x2y - m_x2 * m_y ! Sx2y
b = s_xy * s_x2x2 - s_x2y * s_xx2
b = b / (s_xx * s_x2x2 - s_xx2 * s_xx2)
c = s_x2y * s_xx - s_xy * s_xx2
c = c / (s_xx * s_x2x2 - s_xx2 * s_xx2)
a = m_y - b * m_x - c * m_x2
end subroutine calc_reg_curve
end module comp
program coefficient_of_determination_2d
use const
use comp
implicit none
character(9), parameter :: F_INP = "input.txt"
integer(SP), parameter :: UID = 10
real(DP) :: a, b, c
real(DP) :: y_b, s_r, s_y2, s_e
integer(SP) :: n, i
character(20) :: f
real(DP), allocatable :: x(:), y(:), y_e(:)
! IN ファイル OPEN
open (UID, file = F_INP, status = "old")
! データ数読み込み
read (UID, *) n
! 配列メモリ確保
allocate(x(n))
allocate(y(n))
allocate(y_e(n))
! データ読み込み
do i = 1, n
read (UID, *) x(i), y(i)
end do
write (f, '("(A, ", I0, "F8.2, A)")') n
print f, "説明変数 X = (", x, ")"
print f, "目的変数 Y = (", y, ")"
print '(A)', "---"
! IN ファイル CLOSE
close (UID)
! 単回帰曲線
call calc_reg_curve(x, y, a, b, c)
print '(A, F12.8)', " a = ", a
print '(A, F12.8)', " b = ", b
print '(A, F12.8)', " c = ", c
! 決定係数
y_e = a + b * x + c * x * x ! 推定値
y_b = sum(y) / size(y) ! 標本値 Y (目的変数)の平均
s_r = sum((y_e - y_b)**2) ! 推定値の変動
s_y2 = sum((y - y_b)**2) ! 標本値の変動
s_e = sum((y - y_e)**2) ! 残差の変動
print '(A)', "決定係数"
! 解法-1. 決定係数 (= 推定値の変動 / 標本値の変動)
print '(A, F20.16)', " R2 (1) = ", s_r / s_y2
! 解法-2. 決定係数 (= 1 - 残差の変動 / 標本値の変動)
print '(A, F20.16)', " R2 (2) = ", 1.0 - s_e / s_y2
! 配列メモリ解放
deallocate(x)
deallocate(y)
deallocate(y_e)
end program coefficient_of_determination_2d
3. ソースコードのコンパイル
$ gfortran -o coefficient_of_determination_2d coefficient_of_determination_2d.f95
4. 動作確認
まず、以下のような入力ファイルを用意する。
(先頭行:点の数、2行目以降:各点)
File: input.txt
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14
83 183
71 168
64 171
69 178
69 176
64 172
68 165
59 158
81 183
91 182
57 163
65 175
58 164
62 175
そして、実行。
$ cat input.txt | ./coefficient_of_determination_2d
説明変数 X = ( 83.00 71.00 64.00 69.00 69.00 64.00 68.00 59.00 81.00 91.00 57.00 65.00 58.00 62.00)
目的変数 Y = ( 183.00 168.00 171.00 178.00 176.00 172.00 165.00 158.00 183.00 182.00 163.00 175.00 164.00 175.00)
---
a = 41.37453964
b = 3.08672320
c = -0.01683565
決定係数
R2 (1) = 0.6664619960148396
R2 (2) = 0.6664619960150644
また、参考までに、上記スクリプトで使用した2変量の各点と作成された単回帰曲線を gnuplot で描画してみた。
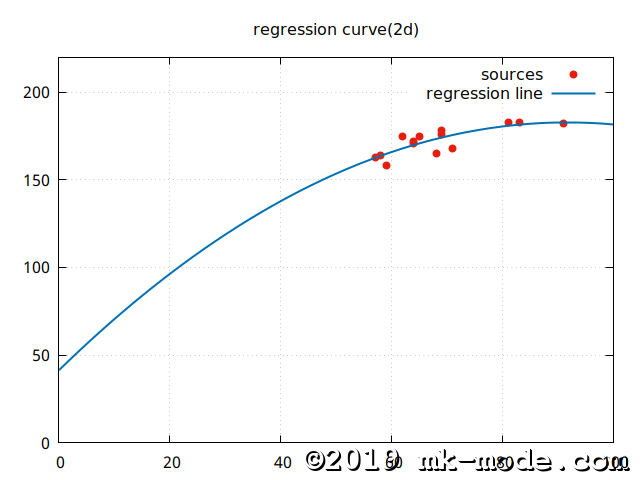
以上。

Comments