C++ - ヒープ生成(上方移動)!
Updated:
今回は「ヒープ」という情報処理試験等でもよく登場する「木(二分木)」のアルゴリズムについてです。
以下、簡単な説明と C++ ソースコードの紹介です。
1. ヒープについて
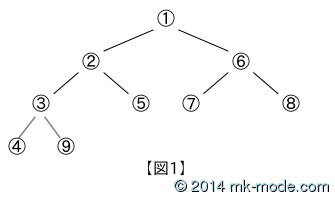
「ヒープ」は「木構造」の一つで、「子要素は親要素より常に大きい(or 小さい)か等しい(子要素の左と右の大小は問わない)」という条件を満足する「完全二分木」である。
以下の【図1】のような構造。
2. ヒープ生成方法(上方移動)
上方移動によるヒープの生成(親要素 < 子要素 の場合)は、以下の【図2】のように最後に追加した要素が親より大きければ交換するという作業を【図1】の状態になるまで繰り返し方法である。(要素を追加する都度生成する方法)
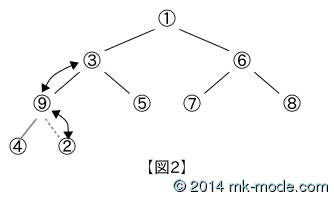
アルゴリズムとしては、
- 上位の親要素から順に配列化して考える。(【図3】)
- 左の子要素の位置を s とすると、親要素の位置 p は s / 2 となる。
- 追加した要素とその親要素を比較し、親要素の方が大きければ子要素と交換する。
- 交換されて親要素になった要素をその親要素と比較して同様に作業を行い、親要素 ≦ 子要素になるまで繰り返す。

3. C++ ソースコード作成
以下のようにソースコードを作成してみた。(要素は乱数で生成)
File: heap_upward.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
/***********************************************************
* ヒープ生成(上方移動)
**********************************************************/
#include <cstdlib> // for srand()
#include <iostream> // for cout
#include <stdio.h> // for printf()
#define N 100 // データ個数
using namespace std;
/*
* ヒープクラス
*/
class Heap
{
// 各種変数
int n, i, s, p, w; // Loop インデックス等
int base[N]; // 元データ用配列
int heap[N + 1]; // ヒープ用配列
public:
Heap(); // コンストラクタ
void generate(); // ヒープ生成
};
/*
* コンストラクタ
*/
Heap::Heap()
{
// ヒープに追加する要素の配列を生成
srand((unsigned int)time(NULL));
printf("#### Base\n");
for (i = 0; i < N; i++) {
base[i] = rand() % N + 1;
printf("%5d ", base[i]);
if ((i + 1) % 10 == 0) printf("\n");
}
printf("\n");
}
/*
* ヒープ生成
*/
void Heap::generate()
{
for (n = 1; n <= N; n++) {
// 元データ配列から1つヒープ要素として追加
heap[n] = base[n - 1];
s = n; // 追加要素の位置
p = s / 2; // 親要素の位置
while (s >= 2 && heap[p] > heap[s]) {
w = heap[p];
heap[p] = heap[s];
heap[s] = w;
s = p; // 追加要素の位置
p = s / 2; // 親要素の位置
}
}
// 結果出力
printf("#### Heap\n");
for (n = 1; n <= N; n++) {
printf("%5d ", heap[n]);
if (n % 10 == 0) printf("\n");
}
printf("\n");
}
/*
* メイン処理
*/
int main()
{
try
{
// ==== インスタンス化
Heap objHeap;
// ==== ヒープ生成
objHeap.generate();
}
catch (...) {
// ==== 異常終了
cout << "例外発生!" << endl;
return -1;
}
// ==== 正常終了
return 0;
}
4. C++ ソースコンパイル
(-Wall は警告出力、-O2 最適化のオプション)
$ g++ -Wall -O2 -o heap_upward heap_upward.cpp
何も出力されなければ成功。
5. 実行
$ ./heap_upward
#### Base
89 85 98 59 63 82 4 76 30 31
4 62 38 77 14 28 93 49 10 21
85 20 20 20 86 12 36 27 22 100
11 10 84 8 20 46 42 23 73 71
5 29 32 95 57 45 22 49 45 84
21 29 55 41 100 40 4 87 67 26
86 77 87 69 36 59 67 77 81 91
99 38 19 30 32 75 26 5 23 22
88 44 2 43 36 1 82 39 39 48
16 24 76 3 45 64 61 63 92 93
#### Heap
1 2 4 5 3 14 11 10 8 4
4 21 20 12 22 36 10 23 19 20
5 20 16 49 45 29 36 27 38 26
77 63 59 77 20 38 30 28 23 30
22 36 29 39 31 24 21 61 59 86
84 62 55 41 100 82 40 87 67 100
86 77 87 89 69 84 67 93 81 91
99 76 42 46 32 75 49 73 26 85
88 71 44 85 43 32 82 95 39 57
48 45 76 22 45 98 64 63 92 93
実際に配列を置き換えてみると、ヒープになっていることが確認できる。
ヒープについて知っておくと、ヒープを使ったソート処理(ヒープ・ソート)を行う際には役立つでしょう。
以上。

Comments