Python - 3次スプライン補間!
Updated:
過去に「3次スプライン補間」を Ruby で実装しました。
今回は、 Python3 で実装してみました。
0. 前提条件
- LMDE 2 (Linux Mint Debian Edition 2; 64bit) での作業を想定。
- Python 3.6.4 での作業を想定。
- グラフ描画に PyPI ライブラリ matplotlib を使用する。
- 当方は他のバージョンとの共存環境であり、
python3.6,pip3.6で 3.6 系を使用するようにしている。(適宜、置き換えて考えること)
1. 3次スプライン補間について
当ブログ過去記事を参照。
2. PyPI ライブラリ matplotlib のインストール
$ sudo pip install matplotlib
3. Python スクリプトの作成
- 敢えてオブジェクト指向で作成している。
- Shebang ストリング(1行目)では、フルパスでコマンド指定している。(当方の慣習)
- 以下のスクリプトでは 0.1 単位で補間するようにしている。
- スクリプト内の定数(
X,Y,S,S_1)は適宜変更すること。
(Sの逆数S_1は、小数刻みでforループする際に浮動小数点の微小誤差を発生させないための措置)
File: spline_interpolation.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
#! /usr/local/bin/python3.6
"""
3-D spline interpolation
(with graph drawing by matplotlib)
"""
import matplotlib.pyplot as plt
import sys
import traceback
class SplineInterpolation:
def __init__(self, xs, ys):
""" Initialization
:param list xs: x-coordinate list of given points
:param list ys: y-coordinate list of given points
"""
self.xs, self.ys = xs, ys
self.n = len(self.xs) - 1
h = self.__calc_h()
w = self.__calc_w(h)
matrix = self.__gen_matrix(h, w)
v = [0] + self.__gauss_jordan(matrix) + [0]
self.b = self.__calc_b(v)
self.a = self.__calc_a(v)
self.d = self.__calc_d()
self.c = self.__calc_c(v)
def interpolate(self, t):
""" Interpolation
:param float t: x-value for a interpolate target
:return float : computated y-value
"""
try:
i = self.__search_i(t)
return self.a[i] * (t - self.xs[i]) ** 3 \
+ self.b[i] * (t - self.xs[i]) ** 2 \
+ self.c[i] * (t - self.xs[i]) \
+ self.d[i]
except Exception as e:
raise
def __calc_h(self):
""" H calculation
:return list: h-values
"""
try:
return [self.xs[i + 1] - self.xs[i] for i in range(self.n)]
except Exception as e:
raise
def __calc_w(self, h):
""" W calculation
:param list h: h-values
:return list : w-values
"""
try:
return [
6 * ((self.ys[i + 1] - self.ys[i]) / h[i]
- (self.ys[i] - self.ys[i - 1]) / h[i - 1])
for i in range(1, self.n)
]
except Exception as e:
raise
def __gen_matrix(self, h, w):
""" Matrix generation
:param list h: h-values
:param list w: w-values
:return list mtx: generated 2-D matrix
"""
mtx = [[0 for _ in range(self.n)] for _ in range(self.n - 1)]
try:
for i in range(self.n - 1):
mtx[i][i] = 2 * (h[i] + h[i + 1])
mtx[i][-1] = w[i]
if i == 0:
continue
mtx[i - 1][i] = h[i]
mtx[i][i - 1] = h[i]
return mtx
except Exception as e:
raise
def __gauss_jordan(self, matrix):
""" Solving of simultaneous linear equations
with Gauss-Jordan's method
:param list mtx: list of 2-D matrix
:return list v: answers list of simultaneous linear equations
"""
v = []
n = self.n - 1
try:
for k in range(n):
p = matrix[k][k]
for j in range(k, n + 1):
matrix[k][j] /= p
for i in range(n):
if i == k:
continue
d = matrix[i][k]
for j in range(k, n + 1):
matrix[i][j] -= d * matrix[k][j]
for row in matrix:
v.append(row[-1])
return v
except Exception as e:
raise
def __calc_a(self, v):
""" A calculation
:param list v: v-values
:return list : a-values
"""
try:
return [
(v[i + 1] - v[i])
/ (6 * (self.xs[i + 1] - self.xs[i]))
for i in range(self.n)
]
except Exception as e:
raise
def __calc_b(self, v):
""" B calculation
:param list v: v-values
:return list : b-values
"""
try:
return [v[i] / 2.0 for i in range(self.n)]
except Exception as e:
raise
def __calc_c(self, v):
""" C calculation
:param list v: v-values
:return list : c-values
"""
try:
return [
(self.ys[i + 1] - self.ys[i]) / (self.xs[i + 1] - self.xs[i]) \
- (self.xs[i + 1] - self.xs[i]) * (2 * v[i] + v[i + 1]) / 6
for i in range(self.n)
]
except Exception as e:
raise
def __calc_d(self):
""" D calculation
:return list: c-values
"""
try:
return self.ys
except Exception as e:
raise
def __search_i(self, t):
""" Index searching
:param float t: t-value
:return int i: index
"""
i, j = 0, len(self.xs) - 1
try:
while i < j:
k = (i + j) // 2
if self.xs[k] < t:
i = k + 1
else:
j = k
if i > 0:
i -= 1
return i
except Exception as e:
raise
class Graph:
def __init__(self, xs_0, ys_0, xs_1, ys_1):
self.xs_0, self.ys_0, self.xs_1, self.ys_1 = xs_0, ys_0, xs_1, ys_1
def plot(self):
""" Graph plotting """
try:
plt.title("3-D Spline Interpolation")
plt.scatter(
self.xs_1, self.ys_1, c = "b",
label = "interpolated points", marker = "+"
)
plt.scatter(
self.xs_0, self.ys_0, c = "r",
label = "given points"
)
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc = 2)
plt.grid(color = "gray", linestyle = "--")
#plt.show()
plt.savefig("spline_interpolation.png")
except Exception as e:
raise
if __name__ == '__main__':
# (N + 1) points
X = [0.0, 2.0, 3.0, 5.0, 7.0, 8.0]
Y = [0.8, 2.8, 3.2, 1.9, 4.5, 2.5]
S = 0.1 # Step for interpolation
S_1 = 1 / S # Inverse of S
xs_g, ys_g = [], [] # List for graph
try:
# 3-D spline interpolation
si = SplineInterpolation(X, Y)
for x in [x / S_1 for x in range(int(X[0] / S), int(X[-1] / S) + 1)]:
y = si.interpolate(x)
print("{:8.4f}, {:8.4f}".format(x, y))
xs_g.append(x)
ys_g.append(y)
# Graph drawing
g = Graph(X, Y, xs_g, ys_g)
g.plot()
except Exception as e:
traceback.print_exc()
sys.exit(1)
3. Python スクリプトの実行
まず、実行権限を付与。
$ chmod +x spline_interpolation.py
そして、実行。
$ ./spline_interpolation.py
0.0000, 0.8000
0.1000, 0.9861
0.2000, 1.1713
0.3000, 1.3544
0.4000, 1.5346
0.5000, 1.7108
0.6000, 1.8820
0.7000, 2.0473
0.8000, 2.2056
0.9000, 2.3559
1.0000, 2.4973
1.1000, 2.6287
1.2000, 2.7492
1.3000, 2.8578
1.4000, 2.9534
1.5000, 3.0351
1.6000, 3.1019
1.7000, 3.1528
1.8000, 3.1868
1.9000, 3.2028
2.0000, 3.2000
2.1000, 3.1782
: :
====< 途中省略>====
: :
7.5000, 2.1279
7.6000, 2.0754
7.7000, 2.0275
7.8000, 1.9831
7.9000, 1.9410
8.0000, 1.9000
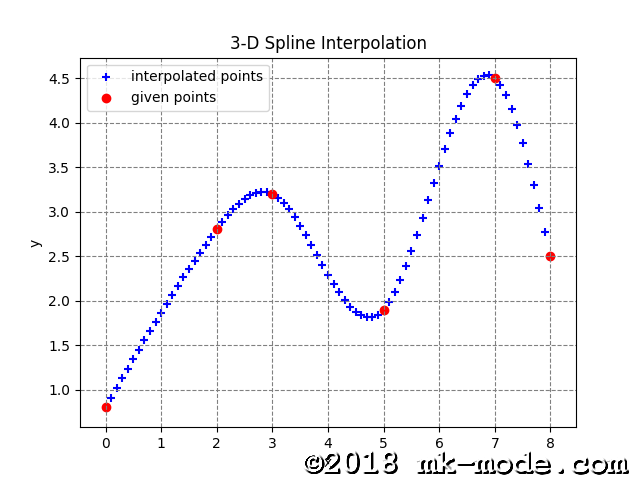
4. グラフ確認
Python スクリプトと同じディレクトリ内に “spline_interpolation.png” という画像ファイルが存在するはずなので、確認してみる。
(赤色の x が予め与えられた点、水色の + が補間された点)
5. 参考サイト
- Ruby - 連立方程式解法(ガウス・ジョルダン法)!(当ブログ過去記事)
以上。

Comments