Ruby - 連立方程式解法(ガウス・ジョルダン(ピボット選択)法)!
Updated:
先日は、連立方程式を「ガウス・ジョルダン法」で解くアルゴリズムを Ruby で実装したことを紹介しました。
また、前回は連立方程式を「ガウス・ジョルダン法」を応用した「ガウス・ジョルダン(ピボット選択)法」で解くアルゴリズムを C++ で実装してみました。
そして、今回はその「ガウス・ジョルダン(ピボット選択)法」で解くアルゴリズムを Ruby で実装してみました。
0. 前提条件
- Linux Mint 14 Nadia (64bit) での作業を想定。
- Ruby 2.0.0-p247 を使用。
- 連立方程式の解法(ガウス・ジョルダン(ピボット選択)法)についての説明は割愛。(「C++ - 連立方程式解法(ガウス・ジョルダン(ピボット選択)法)!」を参照)
1. Ruby スクリプト作成
File: gauss_jorden_pivot.rb
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#! /usr/local/bin/ruby
#***********************************************************
# 連立方程式の解法 ( ガウス・ジョルダン(ピボット選択)法 )
#***********************************************************
#
class GaussJordenPivot
def initialize
# 係数
@a = [
#[ 2, -3, 1, 5],
#[ 1, 1, -1, 2],
#[ 3, 5, -7, 0]
[ 1, -2, 3, -4, 5],
[-2, -5, -8, -3, -9],
[ 5, 4, 7, 1, -1],
[ 9, 7, 3, 5, 4]
]
# 次元の数
@n = @a.size
end
# 計算・結果出力
def exec
# 元の連立方程式をコンソール出力
display_equations
@n.times do |k|
# 行入れ替え
max, s = 0, k
k.upto(@n - 1) do |j|
next unless @a[j][k].abs > max
max = @a[j][k].abs
s = j
end
if max == 0
puts "解けない!"
exit 1
end
(@n + 1).times do |j|
dummy = @a[k][j]
@a[k][j] = @a[s][j]
@a[s][j] = dummy
end
# ピボット係数
p = @a[k][k]
# ピボット行を p で除算
k.upto(@n) { |j| @a[k][j] /= p.to_f }
# ピボット列の掃き出し
@n.times do |i|
next if i == k
d = @a[i][k]
k.upto(@n) { |j| @a[i][j] -= d * @a[k][j] }
end
end
# 結果出力
display_answers
rescue => e
raise
end
private
# 元の連立方程式をコンソール出力
def display_equations
@n.times do |i|
@n.times { |j| printf("%+dx%d ", @a[i][j], j + 1) }
puts "= %+d" % @a[i][@n]
end
rescue => e
raise
end
# 結果出力
def display_answers
@n.times { |k| puts "x%d = %f" % [k + 1, @a[k][@n]] }
rescue => e
raise
end
end
if __FILE__ == $0
begin
# 計算クラスインスタンス化
obj = GaussJordenPivot.new
# 連立方程式を解く(ガウス・ジョルダン(ピボット選択)法)
obj.exec
rescue => e
$stderr.puts "[#{e.class}] #{e.message}"
e.backtrace.each{ |tr| $stderr.puts "\t#{tr}" }
end
end
2. 実行
実際に、次の連立方程式を解いてみる。
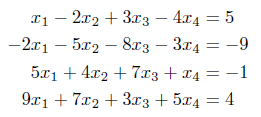
$ ruby gauss_jorden_pivot.rb
+1x1 -2x2 +3x3 -4x4 = +5
-2x1 -5x2 -8x3 -3x4 = -9
+5x1 +4x2 +7x3 +1x4 = -1
+9x1 +7x2 +3x3 +5x4 = +4
x1 = 91.000000
x2 = -349.000000
x3 = 96.000000
x4 = 268.000000
「ガウス・ジョルダン法」に少しだけ処理を追加した程度の内容です。
色々と数値を変えてみたり、元の数を増やしてみるのもよいでしょう。
以上。

Comments