C++ - 多桁乗算(Karatsuba 法)!
Updated:
先日、「標準(筆算)法」による多桁同士の乗算アルゴリズムを C++ に実装してみました。
今回は、「標準(筆算)法」より高速に乗算が可能な「Karatsuba 法」アルゴリズムを C++ で実装してみました。
0. 前提条件
- Linux Mint 14 Nadia (64bit) での作業を想定。
- g++ (Ubuntu/Linaro 4.7.2-2ubuntu1) 4.7.2
また、当方の環境で扱える int 型の範囲は以下のとおり。
int: -2,147,483,648 〜 2,147,483,647
1. Karatsuba 法について
「Karatsuba 法」とは、ロシア人が考案した乗算アルゴリズムで、”Karatsuba” は日本語のように思えるが考案者の名前を英語化したものである。
そして、「Karatsuba 法」の概要は以下のとおり。(数式が多いので\(\TeX\)で記載)

2. C++ ソース作成
例として、以下のようにソースを作成した。概要は以下のとおり。
- 1個の配列で1桁を扱う。
- 計算可能な桁数は 2 のべき乗桁としている。
(2 のべき乗以外の桁数にすると、ロジックが複雑になるため) - 繰り上がり処理は、最後にまとめて行う(但し、非常に大きい乗算桁数では桁あふれを起こすので注意)
- 配列数が4個(桁数が4桁)になったら、標準(筆算)法による乗算を行う。
(4個でなくてもよい。桁溢れしない程度で設定する) - 計算に使用する被乗数・乗数は、手入力は困難なため、乱数を使用している。
- 冒頭の
// #define TESTは、乗算回数をカウントしたり、処理時間を計測するテストを行うため。
テストを行うならコメントを解除する。
(テストの処理時間計測ではclock関数を使用しているため、あまり精度はよくない)
File: multiply_karatsuba.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
/*********************************************
* 多倍長乗算 ( by Karatsuba 法 )
* - 多倍長 * 多倍長
* - 最下位の桁を配列の先頭とする考え方
*********************************************/
#include <cstdlib> // for rand()
#include <iostream> // for cout
#include <math.h> // for pow()
#include <stdio.h> // for printf()
//#define TEST // テスト ( 乗算回数・処理時間 ) するならコメント解除
#define D_MAX 1024 // 計算可能な最大桁数 ( 2のべき乗 )
#define D 1024 // 実際に計算する桁数 ( D_MAX 以下の 4 の倍数 )
using namespace std;
/*
* 計算クラス
*/
class Calc
{
int A[D]; // 被乗数配列
int B[D]; // 乗数配列
#ifdef TEST
int cnt_mul; // 乗算回数
clock_t t1, t2; // 計算開始CPU時刻、計算終了CPU時刻
double tt; // 計算時間
#endif
public:
Calc(); // コンストラクタ
void calcKaratsuba(); // 計算 ( Karatsuba 法 )
private:
void multiplyNormal(int *, int *, int, int *); // 乗算 ( 標準(筆算)法 )
void multiplyKaratsuba(int *, int *, int ,int *); // 乗算 ( Karatsuba 法 )
void doCarry(int *, int); // 繰り上がり・借り処理
void display(int *, int *, int *); // 結果出力
};
/*
* コンストラクタ
*/
Calc::Calc()
{
/* ====================================== *
* テストなので、被乗数・乗数は乱数を使用 *
* ====================================== */
int i; // LOOP インデックス
// 被乗数・乗数桁数設定
for (i = 0; i < D; i++) {
A[i] = rand() % 10;
B[i] = rand() % 10;
}
}
/*
* 計算 ( Karatsuba 法 )
*/
void Calc::calcKaratsuba()
{
int a[D_MAX]; // 被乗数配列
int b[D_MAX]; // 乗数配列
int z[D_MAX * 6]; // 計算結果用配列
int i; // LOOPインデックス
#ifdef TEST
t1 = clock(); // 計算開始時刻
for (int l = 0; l < 1000; l++) {
cnt_mul = 0; // 乗算回数リセット
#endif
// 配列初期設定 ( コンストラクタで設定した配列を設定 )
for (i = 0; i < D; i++) {
a[i] = A[i];
b[i] = B[i];
}
// 最大桁に満たない部分は 0 を設定
for (i = D; i < D_MAX; i++) {
a[i] = 0;
b[i] = 0;
}
// 乗算 ( Karatsuba 法 )
multiplyKaratsuba(a, b, D_MAX, z);
// 繰り上がり・借り処理
doCarry(z, D_MAX * 2);
#ifdef TEST
}
t2 = clock(); // 計算終了時刻
tt = (double)(t2 - t1) / CLOCKS_PER_SEC; // ==== 計算時間
#endif
// 結果出力
display(a, b, z);
}
/*
* 乗算 ( 標準(筆算)法 )
*/
void Calc::multiplyNormal(int *a, int *b, int tLen, int *z)
{
int i, j; // ループインデックス
// 計算結果初期化
for(i = 0; i < tLen * 2; i++) z[i] = 0;
// 各配列を各桁とみなして乗算
for (j = 0; j < tLen; j++) {
for (i = 0; i < tLen; i++) {
z[j + i] += a[i] * b[j];
#ifdef TEST
cnt_mul++; // 乗算カウント
#endif
}
}
}
/*
* 乗算 ( Karatsuba 法 )
*/
void Calc::multiplyKaratsuba(int *a, int *b, int tLen, int *z)
{
// ==== 変数宣言
int *a0 = &a[0]; // 被乗数/右側配列ポインタ
int *a1 = &a[tLen / 2]; // 被乗数/左側配列ポインタ
int *b0 = &b[0]; // 乗数 /右側配列ポインタ
int *b1 = &b[tLen / 2]; // 乗数 /左側配列ポインタ
int *v = &z[tLen * 5]; // v (= a1 + a0) 用配列ポインタ
int *w = &z[tLen * 5 + tLen / 2]; // w (= b1 + b0) 用配列ポインタ
int *x1 = &z[tLen * 0]; // x1 (= a0 * b0) 用配列ポインタ
int *x2 = &z[tLen * 1]; // x2 (= a1 * b1) 用配列ポインタ
int *x3 = &z[tLen * 2]; // x3 (= v * w) 用配列ポインタ
int i; // LOOPインデックス
// ==== 配列が4個になった場合は標準乗算
if (tLen <= 4) {
multiplyNormal(a, b, tLen, z);
return;
}
// ==== v = a1 + a0, w = b1 + b0
for(i = 0; i < tLen / 2; i++) {
v[i] = a1[i] + a0[i];
w[i] = b1[i] + b0[i];
}
// ==== x1 = a0 * b0
multiplyKaratsuba(a0, b0, tLen / 2, x1);
// ==== x2 = a1 * b1
multiplyKaratsuba(a1, b1, tLen / 2, x2);
// ==== x3 = (a1 + a0) * (b1 + b0)
multiplyKaratsuba(v, w, tLen / 2, x3);
// ==== x3 = x3 - x1 - x2
for(i = 0; i < tLen; i++) x3[i] -= x1[i] + x2[i];
// ==== z = x2 * R^2 + (x3 - x2 - x1) * R + x1
// ( x1, x2 は既に所定の位置にセットされているので、x3 のみ加算 )
for(i = 0; i < tLen; i++) z[i + tLen / 2] += x3[i];
}
/*
* 繰り上がり・借り処理
*/
void Calc::doCarry(int *a, int tLen) {
int cr; // 繰り上がり
int i; // ループインデックス
cr = 0;
for(i = 0; i < tLen; i++) {
a[i] += cr;
if(a[i] < 0) {
cr = -(-(a[i] + 1) / 10 + 1);
} else {
cr = a[i] / 10;
}
a[i] -= cr * 10;
}
// オーバーフロー時
if (cr != 0) printf("[ OVERFLOW!! ] %d\n", cr);
}
/*
* 結果出力
*/
void Calc::display(int *a, int *b, int *z)
{
int i; // LOOPインデックス
// 上位桁の不要な 0 を削除するために、配列サイズを取得
int aLen = D_MAX, bLen = D_MAX, zLen = D_MAX * 2;
while (a[aLen - 1] == 0) if (a[aLen - 1] == 0) aLen--;
while (b[bLen - 1] == 0) if (b[bLen - 1] == 0) bLen--;
while (z[zLen - 1] == 0) if (z[zLen - 1] == 0) zLen--;
// a 値
printf("a =\n");
for (i = aLen - 1; i >= 0; i--) {
printf("%d", a[i]);
if ((aLen - i) % 10 == 0) printf(" ");
if ((aLen - i) % 50 == 0) printf("\n");
}
printf("\n");
// b 値
printf("b =\n");
for (i = bLen - 1; i >= 0; i--) {
printf("%d", b[i]);
if ((bLen - i) % 10 == 0) printf(" ");
if ((bLen - i) % 50 == 0) printf("\n");
}
printf("\n");
// z 値
printf("z =\n");
for (i = zLen - 1; i >= 0; i--) {
printf("%d", z[i]);
if ((zLen - i) % 10 == 0) printf(" ");
if ((zLen - i) % 50 == 0) printf("\n");
}
printf("\n\n");
#ifdef TEST
printf("Counts of multiply / 1 loop = %d\n", cnt_mul); // 乗算回数
printf("Total time of all loops = %f seconds\n", tt); // 処理時間
#endif
}
/*
* メイン処理
*/
int main()
{
try
{
// 計算クラスインスタンス化
Calc objCalc;
// 乗算 ( Karatsuba 法 )
objCalc.calcKaratsuba();
}
catch (...) {
cout << "例外発生!" << endl;
return -1;
}
// 正常終了
return 0;
}
3. C++ ソースコンパイル
(-Wall は警告出力、-O2 最適化のオプション)
$ g++ -Wall -O2 -o multiply_karatsuba multiply_karatsuba.cpp
何も出力されなければ成功です。
4. 実行
$ ./multiply_karatsuba
a =
5541050205 0676367860 0766496541 6816500114 2004376325
9767889290 6255254084 0240121540 8107405889 9787092091
5419878423 0874067594 2003014938 3144522637 4398888312
7310798560 7723593059 2397340736 1413730264 5938118523
4930451302 5419027365 4464726284 4804570926 7856292055
6998051538 5419752372 6773282553 8808373348 1147925911
4359623467 7539209376 4653165686 1586483987 2549340871
3021915969 1733401776 8399208132 2374597797 5435289449
3231696299 4733994450 9183503889 6019289550 6163237384
1227614331 9992503157 1308593784 1932936594 0929424801
1950071971 0154922124 5193227045 8846648127 7190389019
7738758027 8658264055 2312943257 6472467201 4300012776
8190966928 1447873191 5142312908 4227930383 4209210656
3795585493 1003705337 6408294366 3725395154 3867977667
2088616184 7174172213 2970374580 1779335759 6608705902
2427117686 6025440760 1301612932 7987359459 5970899460
8046752633 3980870333 6828242461 4139003942 9948802522
0620475091 9136269879 5660460399 9031389202 4282408151
0692857294 5420047984 6336838598 4572973744 3149168608
0328966779 1710456127 7745469624 3867344243 6645626135
8419139297 2271203029 6373
b =
1396721814 7429756767 9697316781 5799720913 8264945924
4078224610 6827742845 2280304370 0503322098 7712258675
0868106360 9153608487 2203105281 1296790491 3736052352
3603808771 3400665829 7092057744 8109671179 4731531344
3030270662 8830811711 2659042336 9560268360 3635996665
4439774037 4364813709 6286856908 2604898197 3917156409
3643090100 1850620740 4921392254 2053171203 9180636269
2516952585 7247460426 4661757895 1691002203 5994933942
3774155041 9930026893 1701001730 3020409083 4387572767
2892156396 8494440010 8636358355 3901596440 6681549762
3712160872 3463720621 7944173552 7388558576 9726708891
6702305518 3009506306 1062776798 5121255133 1714952137
9438940915 6880693386 7752483286 3454240702 0741628501
7609630135 1485681831 5729573433 4022884541 9500149345
9210492650 0111751027 4399813889 9483783897 0746831499
0567300092 4668876475 9172290045 8910594972 4181323728
7410986527 3076964838 8889816294 3754256945 6100329502
4194808714 9521709228 6724065836 1340110964 7865665010
2838147426 9059336788 0834918375 1781651644 0088515395
8991435367 5179991062 2180962809 1488047557 9575103060
4793267825 3098666971 2556
z =
7739305698 0040071707 2189003016 6876576420 6222934577
2023571781 7526420167 7391080311 4489897836 5606748456
8717128396 3330797577 7919515520 8809157391 6002244534
7621606312 5432389533 8866984447 8836029874 7409726049
4007356506 3340487227 9506520886 5423598238 9290074291
2974566830 6442700798 4333021269 4431263626 6374539628
6851995363 4864882970 5572176762 3085210352 4275581437
0897142486 7452815352 0137113684 7907862599 4876133849
0555712981 8780385401 5355569540 8154357653 2471295504
9948804529 3912328019 6503502489 7665018794 4772954562
9490632556 4789219622 8100182409 9768422449 2193203215
2014712520 6011177626 0750743785 4179584096 4152952580
0306309481 6426383088 4574821896 2120453447 6352845378
1951677793 9159184937 5572755307 5303031964 7543670100
5278150467 3261231786 8254099723 7458674159 9839559097
0426560067 4606133160 9122200444 2711896648 1817977034
5524752649 8581262782 1602383986 9796468261 1996639974
2576401764 9436438874 1313980272 5810664985 4229675065
8756237666 5532150529 3593433033 9405077272 1609682116
1412446780 1520707085 6922581219 2890317519 6136848317
5503977733 8847761461 5785599640 3027734783 2267048714
4548525727 8351825512 2431118909 0134095266 6304941694
5445017714 0685438098 2538356667 9630620121 3564506833
4791511337 3608870632 1523183163 7757254037 7900758746
7454636070 9231962770 4771204380 7741285769 9964102181
0886535087 9117351045 4341821086 0872546443 4774459105
1523897188 5238232263 9284079260 9689690063 7880596067
0489076973 1329053634 9696312126 8798891537 2027232304
0211601447 5986863179 6199396248 7964245496 2337368324
3233702362 0325033738 4242202489 2049900204 5559372819
3157276326 8950937657 0461483163 3231712199 0249152697
0627420697 7960887162 9208245972 1570702376 5711273790
4233182037 3921249831 5354876969 9937253686 0092967148
0764175165 1517752657 8361489911 0434806183 4354010504
0070277791 9744702000 8959936173 5978939803 1722903884
7001691849 0262982850 8638795795 0315838055 3558236720
1363881352 6338316728 0294918962 7054187105 8431713068
4930188748 7096773537 8631442377 9673526455 0412143942
3297377182 0841986843 4612914627 7539475285 2246449343
4643618733 2015199866 9194241922 3316370313 5694752406
0784066772 8685693975 1607530824 8097551139 9359388
標準(筆算)法で計算した結果と同じ結果になった。
5. 検証
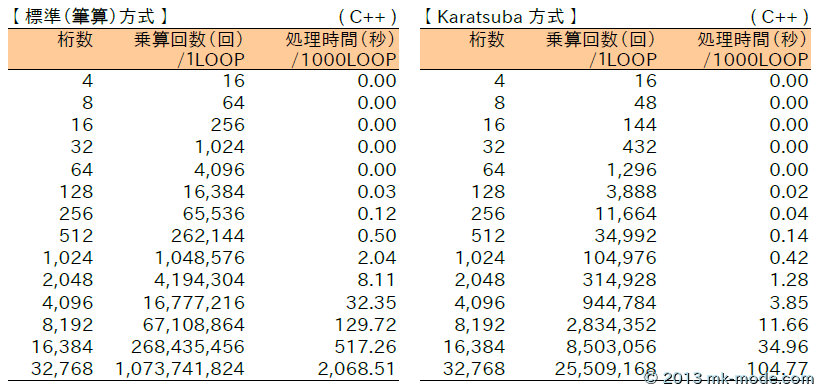
上記のコードを利用して、乗算回数が何回になるか、計算にどれくらい時間がかかるかを検証してみた。
比較のため標準(筆算)法での乗算テスト結果も掲載しているが、標準(筆算)法による乗算より乗算回数は圧倒的に減り、計算に要する時間も圧倒的に短くなった。
ちなみに、再帰的に Karatsuba 法を適用しているので、計算量は単純に\(O(n ^{\log_{2}3})\)にはならない。
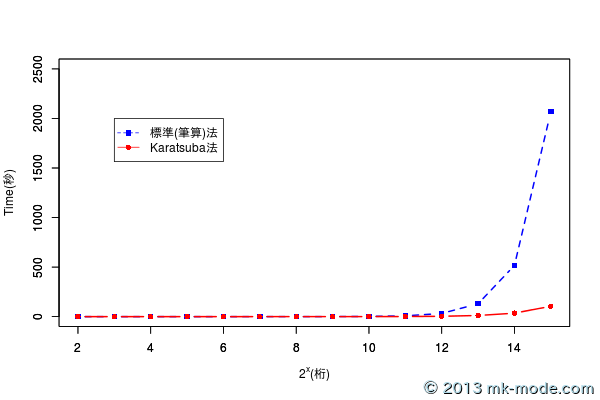
グラフにしてみると、Karatsuba 法が標準(筆算)法より優れているのがよく分かる。
期待通りの結果になり、大変満足です。
やはり、桁数が大きくなればなるほど効果を発揮します。
今回は1桁を1個の配列で扱ったが、乗算する桁数があらかじめ分かっているのなら、1個の配列で4桁を扱ったりすると速度が向上する。(但し、桁あふれに注意)
また、今回は繰り上がり処理を最後にまとめて行なっているが、乗算の都度行うとさらに速度が向上する。(但し、繰り上がりにより配列の個数が変動するので厄介)
このアルゴリズムをどこで使用できるかは、今のところ不明だが、知っておいて悪くないでしょう。
(ちなみに、少し前に当ブログでも紹介した Arctan 系公式を使用した円周率の計算でも、使用する場面は無い)
以上。

Comments