C++ - 非線形方程式の解法（２分法）！

方程式 \(f(x)=0\) の解を２分法により求める C++ アルゴリズム についてです。

まず、１次方程式（つまりグラフ上で直線）以外の方程式を非線形方程式と呼びます。
そして、このような方程式の根を求める方法に「２分法」というものがあります。

アルゴリズムとしては以下のようになります。

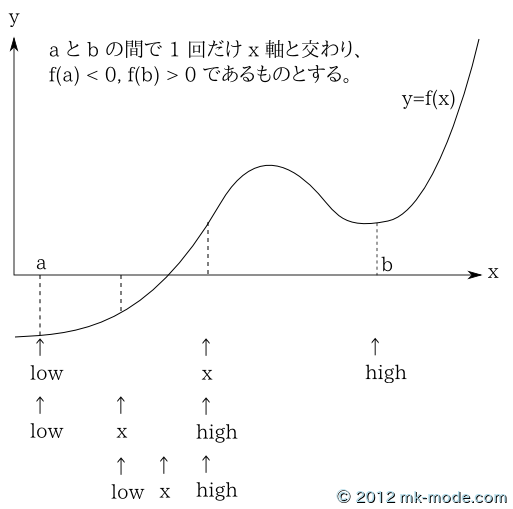
• 根の左右にある２点 a, b を low, high の初期値とする。
• low と high の中点 x を x = (high + low) / 2 で求める。
• f(x) > 0 なら根は x より左にあるから、high = x とし、上限を半分に狭める。
• f(x) < 0 なら根は x より右にあるから、low = x とし、下限を半分に狭める。
• f(x) = 0 か |high - low| / |low| < EPS となった時の x の値を求める根とし、そうでないなら 2. 以降を繰り返す。
  EPS は収束判定値で、適当な精度を選ぶ。

以下、C++ によるサンプルソースです。

0. 前提条件

• Linux Mint 13 Maya (64bit) での作業を想定。
• g++ (Ubuntu/Linaro 4.6.3-1ubuntu5) 4.6.3

1. C++ ソース作成

今回、検証に使用した方程式は、 \(x ^ 3 - x + 1 = 0\) で、グラフは以下のようになる。

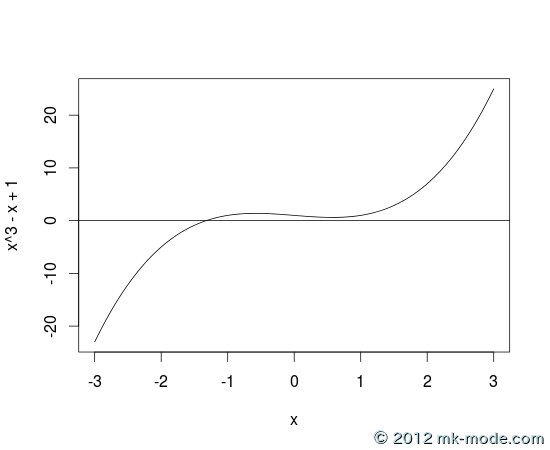
そして、

• C++ なのでオブジェクト指向な作りにしている。
• 収束しない場合は最大50回ループするようにしている。
• f(a) < 0, f(b) > 0 となる方程式を想定。
  f(a) > 0, f(b) < 0 となる方程式の場合は判定部分を修正する必要がある。

File: nonlinear_equation.cpp

/*********************************************
 * 非線形方程式の解法 ( ２分法 )
 *********************************************/
#include <iostream>  // for cout
#include <math.h>    // for fabs()
#include <stdio.h>   // for printf()

// 方程式定義
#define f(x) (x * x * x - x + 1)

using namespace std;

/*
 * 計算クラス
 */
class Calc
{
    // 各種定数
    static const double eps = 1e-08;  // 打ち切り精度
    static const int  limit = 50;     // 打ち切り回数

    // 各種変数
    double low, high, x;  // Low, High, x 値
    int k;                // LOOP インデックス

    public:
        // 非線形方程式を解く（２分法）
        void calcNonlinearEquation();
};

/*
 * 非線形方程式を解く（２分法）
 */
void Calc::calcNonlinearEquation()
{
  // Low, High 初期値設定
  low  = -2.0;
  high =  2.0;

  // 打ち切り回数 or 打ち切り誤差になるまで LOOP
  for (k = 1; k <= limit; k++) {
    x = (low + high) / 2;
    if (f(x) > 0)
      high = x;
    else
      low  = x;
    if (f(x) == 0 || fabs(high - low) / fabs(low) < eps) {
      printf("x=%f\n", x);
      break;
    }
  }

  // 収束しなかった場合
  if (k > limit)
    cout << "収束しない" << endl;
}

/*
 * メイン処理
 */
int main()
{
    try
    {
        // 計算クラスインスタンス化
        Calc objCalc;

        // 非線形方程式を解く（２分法）
        objCalc.calcNonlinearEquation();
    }
    catch (...) {
        cout << "例外発生！" << endl;
        return -1;
    }

    // 正常終了
    return 0;
}

• Gist - C++ source code to compute nonlinear equation with bisection method.

2. C++ ソースコンパイル

$ g++ nonlinear_equation.cpp -o nonlinear_equation

何も出力されなければ成功です。

3. 実行

$ ./nonlinear_equation
x=-1.324718

値を方程式に代入して計算するとほぼ 0 になるので、計算はただしいと考えてよいと思う。

---

数学はおもしろいけど、コンピュータで実証するというのもおもしろいです。

※ちなみに最近の当方の C++ アルゴリズムについての記事は、古い C によるアルゴリズムに関する書物を参考に C++ に移植した形態となっています。

以上。