C++ - 正規乱数(ボックス=ミューラー法)!
Updated:
少し前に、線形合同法を使用して一様乱数を生成する C++ によるアルゴリズムについて紹介しました。
今回は、正規乱数を発生させて実際に正規分布になっているかを検証してみました。
まず、「正規乱数」とは「正規分布」を持つ「乱数」のことです。
「正規分布」は以下のようなグラフになり、
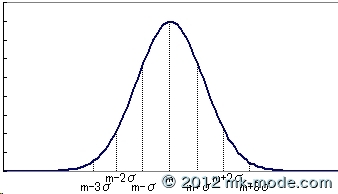
以下のような式で定義されます。
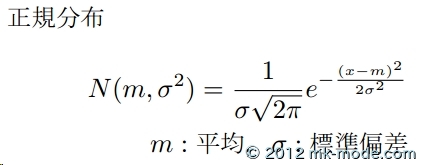
この「正規乱数」の生成方法として、今回は「ボックス=ミューラー法(Box-Muller transform」を使用します。
「ボックス=ミューラー法」は、0 より大きく 1 以下、すなわち (0,1] の一様乱数を正規乱数(正規分布を持つ乱数)に変換する方法で、計算式は以下のようになります。
(0, 1] の2個1組の一様乱数で2個の正規乱数を生成できます。

※正規分布・正規乱数についての詳細は、別途お調べください。
以下、C++ によるサンプルソースです。
0. 前提条件
- Cygwin 1.7.15
- g++ (GCC) 4.7.1
1. C++ ソース作成
今回作成した C++ ソースは以下の通りです。(C++ なのでオブジェクト指向な作りにしている)
また、元となる一様乱数の生成は関数を使用しています。
以下の例では、平均を 10, 標準偏差を 2.5 とし、0 から 20 までの整数乱数に変換して検証しています。
File: rndnum_box_muller.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
/*********************************************
* ボックス=ミューラー法法による正規乱数生成
*********************************************/
#include <iostream> // for cout
#include <math.h> // for cos, sin
#include <cstdlib> // for rand()
#include <stdio.h> // for printf()
using namespace std;
/*
* 計算クラス
*/
class Calc
{
// 各種定数
static const int m = 10; // 平均
static const double s = 2.5; // 標準偏差
static const int n = 10000; // 発生させる乱数の個数
static const double pi = 3.1415926535; // 円周率
// 各種変数
double r1, r2; // 一様乱数
double x, y; // 正規乱数
int hist[m*2+1]; // 件数格納用配列
double scale; // ヒストグラム用スケール
int i, j; // ループインデックス
public:
// コンストラクタ
Calc();
// 正規乱数生成
void generateRndnum();
// 整数乱数
void rnd(double s, double m, double *x, double *y);
// 結果表示
void display();
};
/*
* コンストラクタ
*/
Calc::Calc()
{
// 件数格納用配列初期化
for (i = 0; i <= m * 2; i++) {
hist[i] = 0;
}
// ヒストグラム用スケール
scale = n / 100.0;
}
/*
* 正規乱数生成
*/
void Calc::generateRndnum()
{
// n 回乱数生成処理を繰り返す
for (i = 0; i < n; i++) {
// 整数乱数を2個生成
rnd(s, m, &x, &y);
// 生成された2個の整数乱数を件数格納用配列に格納
hist[(int)x]++;
hist[(int)y]++;
}
}
/*
* 整数乱数
*/
void Calc::rnd(double s, double m, double *x, double *y)
{
// 一様乱数
// ( 32Bitマシンでの (0,1] の実数乱数 )
r1 = rand() / 2147483647.1;
r2 = rand() / 2147483647.1;
// 正規乱数計算
*x = s * sqrt(-2 * log(r1)) * cos(2 * pi * r2) + m;
*y = s * sqrt(-2 * log(r1)) * sin(2 * pi * r2) + m;
}
/*
* 結果表示
*/
void Calc::display()
{
// 0 ~ m * 2 を表示
for (i = 0; i <= m * 2; i++) {
// 件数表示
printf("%3d:%4d | ", i, hist[i]);
// ヒストグラム表示
for (j = 1; j <= hist[i] / scale; j++)
printf("*");
printf("\n");
}
}
/*
* メイン処理
*/
int main()
{
try
{
// 計算クラスインスタンス化
Calc objCalc;
// 正規乱数生成
objCalc.generateRndnum();
// 結果表示
objCalc.display();
}
catch (...) {
cout << "例外発生!" << endl;
return -1;
}
// 正常終了
return 0;
}
今回は32ビットOSでの作業でしたので、(0,1] の一様乱数を生成する際に、rand() 関数の値を int の「最大値+0.1」で除している。
OSが32ビット以外なら int の最大値はこれとは異なる。
2. C++ ソースコンパイル
$ g++ rndnum_box_muller.cpp -o rndnum_box_muller
何も出力されなければ、成功。
3. 実行
$ ./rndnum_box_muller
0: 4 |
1: 12 |
2: 43 |
3: 107 | *
4: 256 | **
5: 626 | ******
6:1207 | ************
7:1939 | *******************
8:2597 | *************************
9:3040 | ******************************
10:3153 | *******************************
11:2744 | ***************************
12:1964 | *******************
13:1201 | ************
14: 617 | ******
15: 320 | ***
16: 121 | *
17: 33 |
18: 9 |
19: 3 |
20: 1 |
4. 判定
出力されたヒストグラムを確認してみると、綺麗な山になっているので正規乱数が正規分布になっていると言えるでしょう。
乱数生成回数をもっと増やしたりしてみてもよいでしょう。
以上。

Comments